Introduction

Resources

• Scala's Types of Types
• A Glossary of Functional Programming

FAQ

What are some of the benefits of Functional Programming?

• Why Functional Programming Matters (Paper)
• Functional Programming Basics
• Functional Programming For The Rest of Us
• The Downfall of Imperative Programming
• Parallelism and concurrency need different tools
• Benefits of Functional Programming
• Programming with Functions

TL;DR

• Pure functions are easier to reason about
• Function signatures are more meaningful
• Parallel/Concurrent programming is easier
• Testing is easier and pure functions lend themselves well to techniques like property-based testing

What is the uniform access principal?

The uniform access principle states that variables, precomputed properties and parameterless functions should be accessed using the same syntax. Therefore not betraying whether they are implemented through storage or through computation.

Scala supports this principle by not allowing parentheses to be placed at call sites of parameterless functions. A parameterless function definition def can be changed to a val or vice versa, without affecting client code

What referentially transparent means?

• Referential Transparency

An expression e is referentially transparent if, for all programs p, all occurrences of e in p can be replaced by the result of evaluating e without affecting the meaning of p

What is a pure function?

A function f is pure if the expression f(x) is referentially transparent for all referentially transparent x. Hence a pure function is modular and composable

What is a higher-order function?

A higher-order function is a function that takes other functions as arguments or returns a function as result

What is a recursive function?

A recursive function is a function which calls itself. With head recursion, the recursive call is not the last instruction in the function

A tail recursive function is a special case of recursion in which the last instruction executed in the method is the recursive call. As long as the recursive call is in tail position, Scala detects and compiles it to the same sort of bytecode as would be emitted for a while loop

def factorial(n: Int): Int = {
  @scala.annotation.tailrec
  def loop(index: Int, result: Int): Int = index match {
    case i if i == 0 =>
      loop(1, 1 * result)
    case i if i < n =>
      loop(i + 1, i * result)
    case i =>
      i * result
  }
  loop(0, 1)
}

factorial(5)
// res0: Int = 120

What is a function literal?

Function literal is a synonyms for anonymous function. Because functions are just ordinary Scala objects, we say that they are first-class values. A function literal is syntactic sugar for an object with a method called apply

val lessThan0 = (a: Int, b: Int) => a < b
// lessThan0: (Int, Int) => Boolean = <function2>
val lessThan1: (Int, Int) => Boolean = (a, b) => a < b
// lessThan1: (Int, Int) => Boolean = <function2>
val lessThan2 = new Function2[Int, Int, Boolean] {
  override def apply(a: Int, b: Int): Boolean = a < b
}
// lessThan2: (Int, Int) => Boolean = <function2>

How for-comprehensions is desugared?

• For Comprehensions (Documentation)

// (1) works because "foreach" is defined
for (i <- List(1, 2, 3)) println(i)
// 1
// 2
// 3
List(1, 2, 3).foreach(println)
// 1
// 2
// 3

// (2) "yield" works because "map" is defined
for (i <- List(1, 2, 3)) yield i * 2
// res3: List[Int] = List(2, 4, 6)
List(1, 2, 3).map(_ * 2)
// res4: List[Int] = List(2, 4, 6)

// (3) "if" works because "withFilter" is defined
for (i <- List(1, 2, 3, 4); if i % 2 == 0) yield i * 2
// res5: List[Int] = List(4, 8)
List(1, 2, 3, 4).withFilter(_ % 2 == 0).map(_ * 2)
// res6: List[Int] = List(4, 8)

// (4) works because "flatMap" is defined
for (i <- List(1, 2, 3, 4); j <- List(3, 4, 5, 6); if i == j) yield i
// res7: List[Int] = List(3, 4)
List(1, 2, 3, 4).flatMap(i =>
  List(3, 4, 5, 6).flatMap(j =>
    if (i == j) List(i)
    else List.empty[Int]
  )
).map(i => i)
// res8: List[Int] = List(3, 4)

What is an algebraic data type?

• Algebraic Data Types in Scala
• What the Heck are Algebraic Data Types?

In type theory, regular data structures can be described in terms of sums, products and recursive types. This leads to an algebra for describing data structures (and so-called algebraic data types). Such data types are common in statically typed functional languages

An algebraic data type (ADT) is just a data type defined by one or more data constructors, each of which may contain zero or more arguments. The data type is the sum / union / coproduct of its data constructors usually represented using sealed traits, and each data constructor is the product of its arguments typically represented using case classes, hence the name algebraic data type

Example

• these types represent a sum type because Shape is a Circle or a Rectangle
• Circle is a product type because it has a radius
• Rectangle is a product type because it has a width and a height

sealed trait Shape
final case class Circle(radius: Double) extends Shape
final case class Rectangle(width: Double, height: Double) extends Shape

Sum types and product types provide the necessary abstraction for structuring various data of a domain model. Whereas sum types let model the variations within a particular data type, product types help cluster related data into a larger abstraction

An API should form an algebra — that is, a collection of data types, functions over these data types, and importantly, laws or properties that express relationships between these functions

What are inhabitants of a type?

Inhabitants of a type are values for that types. Algebraic Data Types can be thought of in terms of regular algebraic equations and its result gives the number of inhabitants

• sum types: Either[A, B] or A or B corresponds to the equation A + B
• products types: (A, B) or Tuple2 or A and B corresponds to the equation A * B
• exponentiation: A -> B or Function1 corresponds to the equation B ^ A
  • e.g. Boolean -> Boolean is 2 ^ 2
• the Unit data type corresponds to the value 1
• the Void data type corresponds to the value 0

TODO What is morphism?

TODO

• Morphism
• Closures and universal quantification

A function having the same argument and return type is sometimes called an endofunction

What is polymorphism?

• What is polymorphism?
• Polymorphism, and typeclasses in Scala
• Polymorphism in Scala
• How to be polymorphic in Scala
• How to make ad-hoc polymorphism less ad hoc (Paper)(Haskell)

A polymorphic type is the one whose operations can be applied to other types

In Sub-typing Polymorphism a type (sub-type) is related to another (super-type) in a way where operations that apply to the super-type can also apply to its sub-types i.e. when a type inherits from another

In Parametric Polymorphism types, methods or functions can be written generically using Type Parameters so they can handle values without depending on their types

In Ad-hoc Polymorphism, known as method or function overloading, the compiler applies argument of different types to functions or methods and decide which implementation is the correct to use, depending on the type of the arguments to which they are applied

What is the difference between monomorphic and polymorphic?

• Method-level parametric polymorphism

Monomorphic methods can only be applied to arguments of the fixed types specified in their signatures, whereas polymorphic methods can be applied to arguments of any types which correspond to acceptable choices for their type parameters

// monomorphic methods have type parameter-free signatures
def monomorphic(s: String): Int = s.length

// only values of type String
monomorphic("hello")
// res9: Int = 5

// polymorphic methods have type parameters in their signatures
def polymorphic[T](list: List[T]): Int = list.length

polymorphic(List(1, 2, 3))
// res10: Int = 3
polymorphic(List("foo", "bar", "baz"))
// res11: Int = 3

Only by knowing the type signature of a method is possible to infer more or less information regarding its underlying implementation

• given a monomorphic signature List[Int] -> List[Int], there are too many possible implementations to say what the function does
• given a polymorphic/parametrized type signature List[A] -> List[A], it's proven that all elements in the result must appear in the input if there are not side effects, which restricts the number of possible implementations

TODO How does the implicit resolution mechanism work?

TODO

• Implicits, type classes, and extension methods
• revisiting implicits without import tax
• implicit parameter precedence again
• Where does Scala look for implicits?

TODO see slides (1)

• Implicit parameters
• Implicit values
• Implicit conversions
• Implicit classes

TODO What is a context bound?

TODO

• What are Scala context bounds? (Documentation)
• What are Scala context and view bounds?

// context bound
def f[A : Ordering](a: A, b: A) = implicitly[Ordering[A]].compare(a, b)

// implicit evidence
def f[A](a: A, b: A)(implicit ev: Ordering[A]) = ev.compare(a, b)

What is a type class?

• Type Classes as Objects and Implicits (Paper)
• Type classes in Scala
• Returning the "Current" Type in Scala
• Typeclass 101: ad hoc polymorphism in scala
• All you don't need to know about Typeclasses
• Scala Implicits : Type Classes Here I Come
• A Small Example of the Typeclass Pattern in Scala
• Typeclasses 101
• Scala/Haskell: A simple example of type classes

A Type Class is a type system construct that supports ad-hoc polymorphism and is achieved by adding constraints to type variables in parametrically polymorphic types

It's a programming pattern that allow to extend existing libraries with new functionality, without using traditional inheritance and without altering the original library source code using a combination of ad-hoc polymorphism, parametric polymorphism (type parameters) and implicits

What are type constructors and higher-kinded types?

• Generics of a Higher Kind (Paper)
• Fighting Bit Rot with Types (Paper)
• Kinds and some type-foo
• What is a higher kinded type in Scala?
• Type Constructor Polymorphism
• Scala: Types of a higher kind

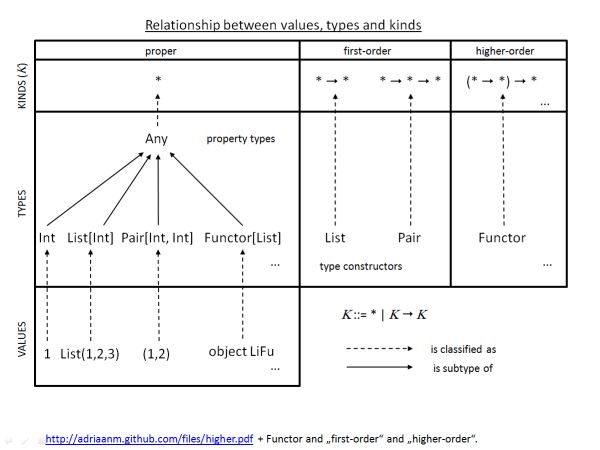
Type Constructors act like functions, but on the type level

• 42 is a proper value
• Int is a proper type *
• def f[A](a: A) = ??? is a function that takes a type parameter A
  • f is a value constructor
  • f has an abstract/polymorphic type parameter A of first-order
  • A is of first-order because it cannot abstract over anything e.g. Java generics
• List is a type constructor
• List[Int] is a concrete type
• List[+A] is a type constructor that takes a type parameter A
  • List is a first-order-kinded type * -> *
• Either is a type constructor that takes two type parameters A and B
  • Either is a first-order-kinded type * -> * -> *
• in M[F[_]], the M is a type constructor that takes a type constructor parameter F
  • M is a higher-kinded or higher-order type (* -> *) -> *

scala> :kind -v Int
Int's kind is A
*
This is a proper type.

scala> :kind -v List
List's kind is F[+A]
* -(+)-> *
This is a type constructor: a 1st-order-kinded type.

scala> :kind -v Either
Either's kind is F[+A1,+A2]
* -(+)-> * -(+)-> *
This is a type constructor: a 1st-order-kinded type.

scala> trait M[F[_]]
scala> :kind -v M
M's kind is X[F[A]]
(* -> *) -> *
This is a type constructor that takes type constructor(s): a higher-kinded type.

TODO parallel between curried (function) and type constructor - see Arrows in category theory

What are singleton types?

In a companion object

object Foo
Foo
// res12: Foo.type = repl.MdocSession$App$Foo$@58dee316

The singleton type Foo.type is the type of Foo, and Foo is the only value with that type

What are literal types?

A Scala literal value may have multiple types

"foo": String
// res13: String = "foo"
"foo": AnyRef
// res14: AnyRef = "foo"
"foo": Any
// res15: Any = "foo"

Literal values have also another type: a singleton type that belongs exclusively to that one value. Singleton types applied to literal values are called literal types

Unfortunately the default behaviour of the compiler is to widen literals to their nearest non-singleton type, making these two expressions equivalent

"foo"
// res16: String = "foo"
"foo" : String
// res17: String = "foo"

It's possible to convert a literal expression to a singleton-typed literal expression with narrow

import shapeless.syntax.singleton.mkSingletonOps

val x = "foo".narrow
// x: String("foo") = foo

TODO What are phantom types and type tagging?

TODO

• Phantom Types in Scala

A literal number is an Int in two worlds: at runtime, where it has an actual value and methods that can be called, and at compile time, where the compiler uses the type to calculate which pieces of code work together and to search for implicits

val number = 42
// number: Int = 42

trait Answer
val myAnswer = number.asInstanceOf[Int with Answer]
// myAnswer: Int with Answer = 42

It's possible to modify the type of number at compile time without modifying its runtime behaviour by tagging it with a phantom type. Phantom types are types with no runtime semantics

TODO What are existential types?

TODO

• Existential types

TODO What is a type lambda?

TODO

• Type lambdas and kind projector
• Type Lambda in Scala
• What are type lambdas in Scala and what are their benefits?
• kind-projector

TODO What are type members?

TODO

• Type Parameters and Type Members (type projector ???)

What are dependent types?

• Dependent Types in Scala

trait Generic[A] {
  type R
  def to(value: A): R
  def from(value: R): A
}

object Generic {
  def getR[A](value: A)(implicit gen: Generic[A]) = gen.to(value)
}

Given the definition above, where A is a type parameter and R is a type member, getR will return a type that depends on gen instance i.e. its value parameter via the type member

TODO What is type erasure?

TODO

• Overcoming type erasure in Scala
• Type Erasure in Scala

trait Test
case class Test1() extends Test
case class Test2() extends Test

@scala.annotation.nowarn
def check1[T <: Test](test: Test):Boolean =
  test.isInstanceOf[T]

def check2[T <: Test: scala.reflect.ClassTag](test: Test): Boolean =
  test match {
    case _: T => true
    case _ => false
  }

// it does NOT work
check1[Test1](Test1())
// res18: Boolean = true
check1[Test1](Test2())
// res19: Boolean = true
check1[Test2](Test1())
// res20: Boolean = true

// it works
check2[Test1](Test1())
// res21: Boolean = true
check2[Test1](Test2())
// res22: Boolean = false
check2[Test2](Test1())
// res23: Boolean = false

What is an effectful computation?

In functional programming, an effect adds some capabilities to a computation. An effect is modeled usually in the form of a type constructor that constructs types with these additional capabilities

• List[A] adds the effect of aggregation on A
• Option[A] adds the capability of optionality for the type A
• Try[A] models the effects of exceptions